Прямая

Для определения положения прямой в пространстве существуют следующие методы:

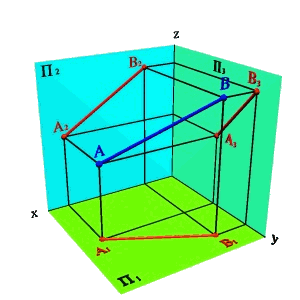
1.Двумя точками (А и В).

 Рассмотрим две точки в пространстве А и В (рис. 7). Через эти точки можно провести прямую линию. Для того чтобы найти проекции отрезка [AB] на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка: 

[A1B1]<[AB]; [A2B2]<[AB]; [A3B3]<[AB].

 

  

 

 

 

 

 

 

 

 

 

 

 

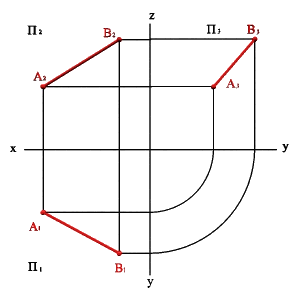
                   а) модель                                                        б) эпюр

Рисунок 7.Определение положения прямой по двум точкам

 

Обозначим углы между прямой и плоскостями проекций через α- с плоскостью П1, β- с плоскостью П2, γ- с плоскостью П3 и тогда получим:

|А1В1|=|AB|cos a

|A2B2|=|AB|cos b

|A3B3|=|AB|cos g.

Частный случай |A1B1|=|A2B2|=|A3B3| при таком соотношении прямая образует с плоскостями проекций равные между собой углы a=b=g=350, при этом каждая из проекций расположена под углом 450 к соответствующим осям проекций.

2. Двумя плоскостями (a; b).

Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).

3. Двумя проекциями.

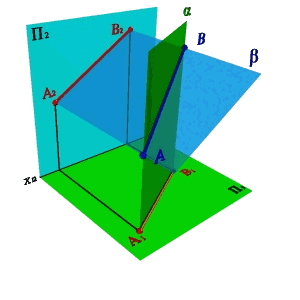
Пусть в плоскостях П1  и П2 даны проекции прямых заданных отрезками [А1В1] и [A2B2]. Проведем через эти прямые плоскости a и bперпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис.8а), линией их пересечения будет прямая заданная отрезком [АВ], проекциями которой являются отрезки [А1В1] и [А2В2].

 

  

  

  

 

 

 

 

 

 

  

 

         

 

            а) a непараллельная b                                  б) a и b совпадают

Рисунок 8.Определение положения прямой в пространстве по двум проекциям отрезка

 

Плоскости  a и b могут слиться в одну плоскость g, если, например, проекции [А1В1] и [А2В2]перпендикулярны оси x  и пересекают ее в одной точке (рис.8б). Прямая линия в этом случае будет однозначно определена своими проекциями, если на каждой из них обозначить две какие-либо точки. Если же обозначений не делать, то за искомую прямую можно принять любую прямую, лежащую в этой  плоскости при условии, что она непараллельная ни одной из плоскостей проекций. Точка К, в данном случае - точка пересечения прямой с плоскостью П2.

4. Точкой и углами наклона к плоскостям проекций.

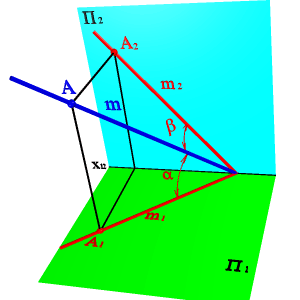
Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве(рис.9)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 9. Определение положения прямой по точке и углам наклона к плоскостям проекций

.