Кривые линии 

Кривая линия - это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая» в разных разделах математики определяется по-разному.

 В начертательной геометрии кривую рассматривают как траекторию, описанную движущей точкой, как проекцию другой кривой, как линию пересечения двух поверхностей, как множество точек, обладающих каким-либо общим для всех их свойством и т.д.

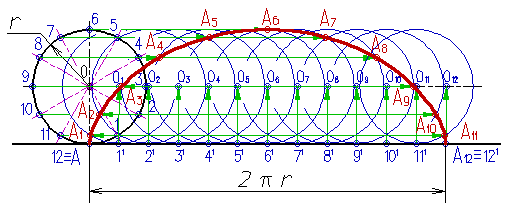
Например, (рис.15) циклоида – траектория движения точки окружности, катящейся без скольжения по прямой линии. Эта кривая состоит их ряда «арок», каждая из которых соответствует полному обороту окружности.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 15. Циклоида

 

Каждая кривая включает в себя геометрические элементы, которые составляют её определитель, т.е. совокупность независимых условий, однозначно определяющих эту кривую.

Различны и способы задания кривых:

· аналитический – кривая задана математическим уравнением;

· графический – кривая задана визуально на носителе графической информации;

· табличный – кривая задана координатами последовательного ряда точек.

Уравнением кривой линии называется такое соотношение между переменными, которому удовлетворяют координаты точки, принадлежащей кривой.

В основу классификации кривых положена природа их уравнений.

Кривые подразделяются на алгебраические и трансцендентные в зависимости от того, являются ли их уравнения алгебраическими или трансцендентными в прямоугольной системе координат.

Плоская кривая линия называется алгебраической, если её уравнение f (xy)=0. Функция  f (xy) является степенным множителем относительно переменных х и у; в остальных случаях кривая называется трансцендентной.

Кривая линия, представленная в декартовых координатах уравнением п-й степени, называется алгебраической кривой п-го порядка.

Кривые линии, все точки которых принадлежат одной плоскости, называются плоскими, остальные пространственными.